구조
그래프는 정점(vertex)과 간선(edge)으로 이루어진 구조입니다. 이는 지하철의 노선도와 비슷한 개념이기도 합니다. 지하철의 노선도처럼 정점과 정점사이의 최적의 경로를 알 수도 있습니다.
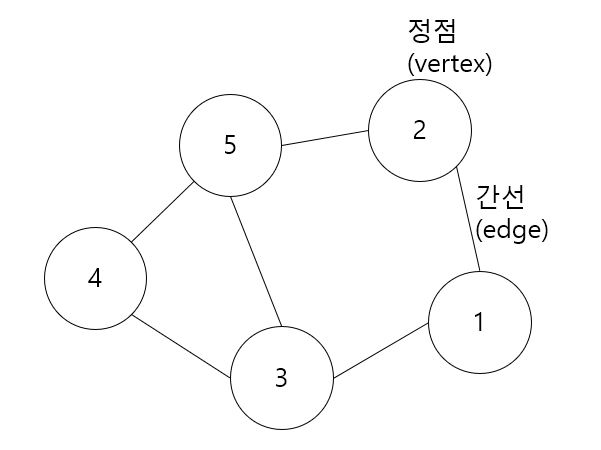
종류
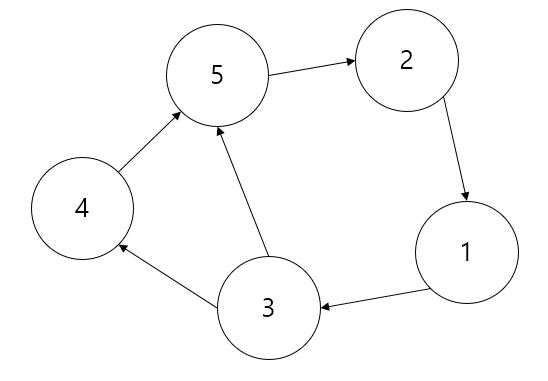
- 방향 그래프 (directed graph); 다이그래프 (digraph)
- 방향에 대한 정보가 그려진 그래프입니다.
- 이와 반대로 방향이 없는 무방향 그래프(undirected graph)가 있습니다.
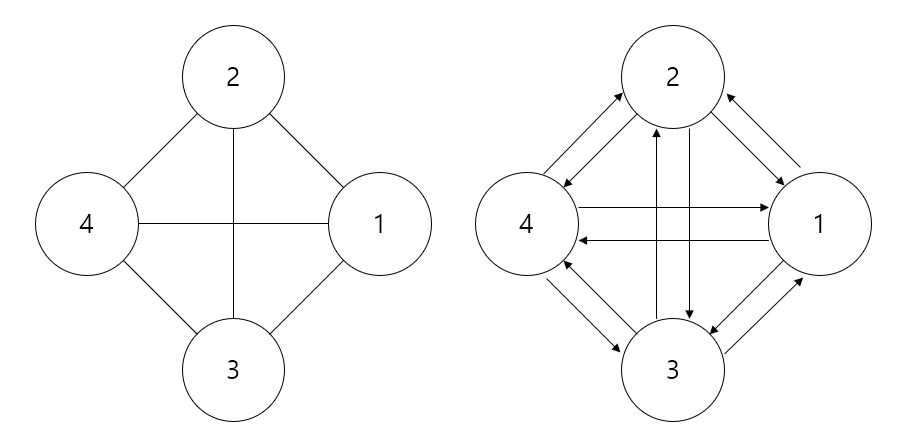
- 완전 그래프 (complete graph)
- 모든 정점이 자신을 제외한 모든 정점을 연결한 그래프입니다.
- 방향 그래프는 모든 정점을 가리켜야하므로 두 정점당 2개의 간선이 나타납니다.
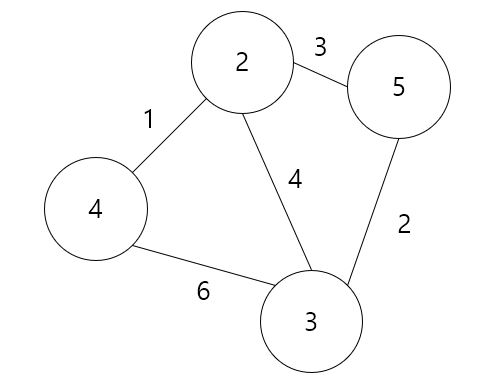
- 가중치 그래프 (weight graph)
- 간선에 가중치에 대한 정보를 표시하여 구성한 그래프입니다.
- 가중치의 의미는 이동시간으로 둘 수도 있고, 그 외의 정보로 설정할 수도 있습니다.
- 부분 그래프 (sub graph)
- 그래프의 일부만 표현한 그래프입니다.
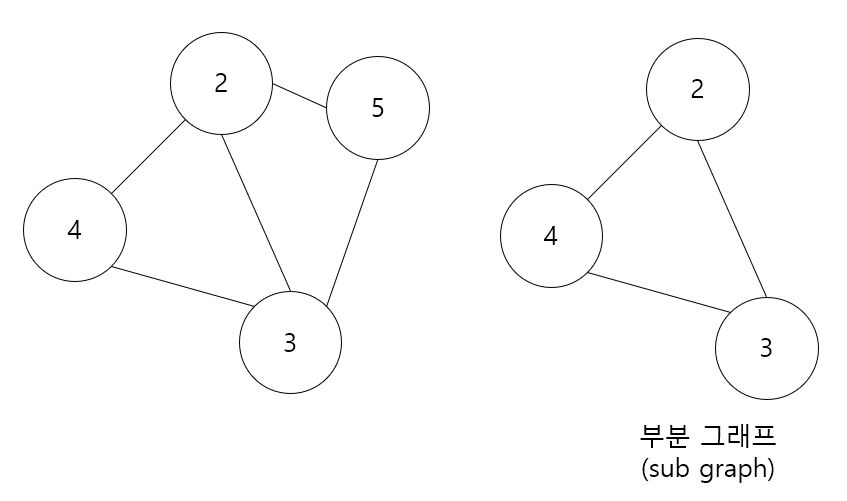
- 그래프의 일부만 표현한 그래프입니다.
표현
- 무방향 그래프의 표현
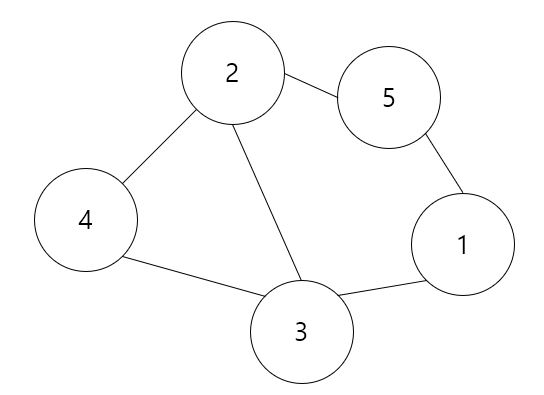
- 정점 : V(G) = {1, 2, 3, 4, 5} (G는 그래프 이름)
- 간선 : E(G) = {(4, 2), (4, 3), (2, 5), (5, 1), (3, 1), (2, 3)} (G는 그래프 이름)
- 방향 그래프의 표현
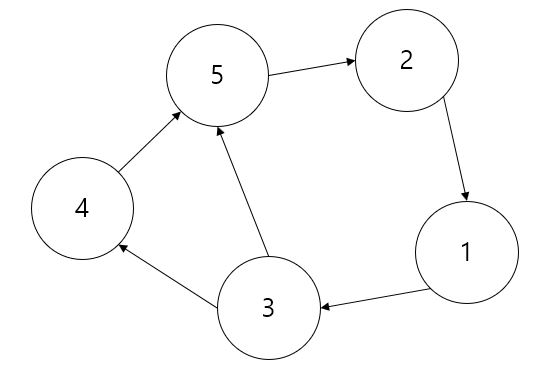
- 정점 : V(G) = {1, 2, 3, 4, 5} (G는 그래프 이름)
- 간선 : E(G) = {<3, 4>, <4, 5>, <3, 5>, <5, 2>, <2, 1>, <1, 3>} (G는 그래프 이름)
- <A, B> : A가 B를 가리키는 간선
소스 코드 (인접 리스트(adjacent list)기반 그래프)
Graph.h
#pragma once
#include <iostream>
#include <vector>
using namespace std;
class graph
{
private:
vector<pair<int, int>> *pgraph = nullptr;
int count_edge = 0;
public:
graph() = delete;
graph(int vertex) { pgraph = new vector<pair<int, int>>[vertex]; }
~graph() { delete[] pgraph; }
void add(int from_vertex, int to_vertex)
{
pgraph[from_vertex].push_back(to_vertex);
}
void show() const
{
for (int i = 0; i < count_edge + 1; i++)
{
if(pgraph[i].empty())
{
cout << i << "is nothing connected" << endl;
continue;
}
typename vector<int>::iterator it;
cout << i << " is connected with";
for (it = pgraph[i].begin(); it != pgraph[i].end(); it++)
{
cout << ' ' << *it;
if(it == pgraph[i].end() - 1)
break;
cout << ',';
}
cout << endl;
}
}
const int size_vertex() const { return count_edge + 1; }
const int size_edge() const { return count_edge; }
};Graph.cpp
#include <iostream>
#include "Graph.h"
using namespace std;
int main()
{
graph g(5);
g.add(0, 1);
g.add(0, 3);
g.add(1, 2);
g.add(2, 3);
g.add(3, 4);
g.add(4, 0);
g.show();
return 0;
}'알고리즘 Algorithm > 자료구조 Data structure' 카테고리의 다른 글
| 최소 비용 신장 트리 (Minimum cost Spanning Tree; MST) (0) | 2021.03.31 |
|---|---|
| DFS (깊이 우선 탐색) | BFS (너비 우선 탐색) (0) | 2021.03.28 |
| 테이블 (Table) : 체이닝 (Chaining) (0) | 2021.03.25 |
| 테이블 (Table) : Key & Value, Hash (해쉬), Collision (충돌) (0) | 2021.03.24 |
| 탐색 (Search) : AVL 트리 (AVL Tree) (0) | 2021.03.22 |



